VIDEO

SEGUN SUS ÁGULOS

Polígonos cóncavos; son aquellos que tiene un ángulo interior mayor que 180º

Polígonos convexos; son aquellos cuyos ángulos interiores son menores que 180º.      

 Polígonos regulares; son aquellos cuyos lados y ángulos interiores tienen igual medida.                

ELEMENTOS DE UN POLÍGONO REGULAR:

Centro

Punto interior que equidista de cada vértice

Radio

Es el segmento que va del centro a cada vértice.

Apotema

Distancia del centro al punto medio de un lado

Polígonos irregulares; son aquellos cuando la medida de sus lados  o de sus ángulos  son diferentes.

                                        

POLIGONOS

ESTANDARES:

1.Identifica y clasifica los polígonos y sus partes, y deduce sus propiedades fundamentales.

2. Distingue entre polígonos cóncavos y convexos

3. Clasifica y reconoce los triángulos y los cuadriláteros.

COMPETENCIA: Capacidad de ubicarse en el espacio para establecer relaciones físicas y gráficas con entes geométricos.

INDICADORES DE LOGROS:

1. Reconoce los elementos de un polígono.

2. Diferencia polígonos convexos y cóncavos.

3. Identifica polígonos regulares.

4. Identifica y construye triángulos, según ciertas condiciones dadas.

5. Identifica cuadriláteros y sus características  específicas.

6. Calcula la medida de un ángulo interior y la suma de la medida de los ángulos interiores de un polígono regular.

CONOCIMIENTO PREVIO:

1. ¿Qué es un polígono para usted?

2. ¿Cuáles son los elementos de un polígono?

3. ¿Cuántas clases de polígonos conoce usted?

4. ¿Qué es un triángulo? ¿Qué es un cuadrilátero?

CONOCIMIENTOS BÁSICOS:

POLIGONOS

Un polígono es una figura geométrica formada por segmentos de rectas, de tal manera que no se cruzan y tienen sólo los puntos extremos comunes. Ejemplos

Elementos de un polígono

En todo polígono se pueden identificar los siguientes elementos:

Lados: Son los segmentos que lo limitan.

Vértices: Son los puntos donde concurren dos lados.

Ángulos interiores de un polígono: Son los determinados por dos lados consecutivos.

Suma de ángulos interiores de un polígono: Si n es el número de lados de un polígono: 

Suma de ángulos de un polígono = (n − 2) ·180°  

Diagonal: Son los segmentos que determinan dos vértices no consecutivos.

Número de diagonales de un polígono

Si n es el número de lados de un polígono: Número de diagonales = n · (n − 3) / 2

5. (5-3)/2= 5

6.(6-3)/2= 9

4.(4-3)/2= 2

Angulo Exterior:es el formado por los segmentos de rectas que parten del centro a los extremos de un lado; este se determina dividiendo 360º por el número de lados del polígono, y el ángulo externo es el formado por un lado y la prolongación de un lado consecutivo o podemos aplicar 180º - ángulo interno

Clases de polígonos

Según sus lados: los polígonos reciben nombres especiales  de acuerdo con el número de lados que tengan:

 

• Triángulos — los que tienen 3 lados y 3 ángulos.
• Cuadriláteros — los que tienen 4 lados y 4 ángulos.
• Pentágonos (del griego: penta: cinco) — los que tienen 5 lados y 5 ángulos.
• Exágonos (del griego: exa: seis) — los que tienen 6 lados y 6 ángulos.
• Heptágonos (del griego: hepta: siete) — los que tienen 7 lados y 7 ángulos.
• Octógonos — los que tienen 8 lados y 8 ángulos.
• Encágonos — los que tienen 9 lados y 9 ángulos.
• Decágonos — los que tienen 10 lados y 10 ángulos.
• Undecágonos — los que tienen 11 lados y 11 ángulos.
• Dodecágonos — los que tienen 12 lados y 12 ángulos.
  
  Con más de 12 lados, se denominan indicando el número de lados.

Realiza: dar click aquí

CLASES DE ANGULOS

Los ángulos pueden clasificarse según su medida, su posición y su suma.

1.   Según su medida los ángulos pueden ser: a. Agudos, son aquellos cuya medida es menor de 90º

b. Rectos, son aquellos cuya medida es igual a 90º

c. Obtusos, son aquellos cuya medida es mayor de 90º y menor de 180º.

2. Según su posición los ángulos pueden ser:

a. Consecutivos, dos ángulos son consecutivos cuando están en un mismo plano, tienen el mismo vértice, un lado común y los lados no comunes quedan en distintos semiplanos respecto del lado común.

 

b. Adyacentes,dos ángulos son adyacentes cuando son consecutivo y los lados no comunes forman una línea recta.

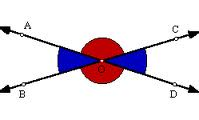
c. Opuestos por el vértice, Son ángulos que tienen el vértice común y los lados de cada uno de ellos son la prolongación de los del otro.

 

3. Según su suma los ángulos pueden ser:

a. Complementarios;  dos ángulos son complementarios si sus medidas suman 90º                              

b. Suplementarios, dos ángulos son suplementarios si sus medidas suman 180º.

VIDEO GEOMETRIA Y NATURALEZA

LA GEOMETRIA QUE NOS ENSEÑA LA NATURALEZA

Varios matemáticos y filósofos, impresionados por la belleza y elegancia lógica de la geometria, han pretendido utilizar las ideas geométricas para explicar el Universo en que vivimos. Uno de los primeros fue Platón, el cual estaba tan prendado de los cinco sólidos regulares que los empleó como la base de una teoria de la materia. En su libro Timeo, escrito hacia el 350 a. C., Platón llevó adelante la sugerencia de que los "cuatro" elementos que se pensaba que componian mundo -el agua, el aire, el agua y la tierra- eran todos ellos agregados sólidos diminutos. Pensaba además que, puesto que el mundo solamente podía estar formado a partir de cuerpos perfectos, tales elementos debían tener la forma de los sólidos regulares. Según Platon, el fuego debe ser un tetraedro al ser el más ligero y punzante de los elementos, la tierra ha de consistir en cubos al ser el más estable de todos, el agua debe ser un icosaedro, el sólido regular que tiene más posibilidades de rodar facilmente, por ser el más móvil y fluido y en cuanto al aire, Platón observó que "el aire es al agua lo que el agua es a la tierra", y concluyó, aunque algo misteriosamente, que el aire debe ser un octaedro. Y finalmente, para no dejar al único sólido regular que queda fuera del cuadro, propuso que el dodecaedro representara la forma del Universo en su totalidad.

VIDEOS

CONGRUENCIA DE ANGULOS

Dos ángulos son congruentes si tienen la misma medida, sin importar la posición ni la longitud de sus lados.                                                                         

< DAC  es congruente con < FBE

Bisectriz de un ángulo  

La bisectriz de un ángulo es una semirrecta que partiendo del vértice del ángulo  lo divide  en dos ángulos congruentes.

MEDICION DE ANGULOS

La medida de un ángulo está determinada por la amplitud entre sus lados, pero no depende de su longitud. Una unidad de medida es el grado sexagesimal. Se simboliza º

El instrumento que se usa para medir ángulos es el transportador.

Para medir un ángulo, se hace coincidir el centro del transportador con el vértice del ángulo y el cero del transportador con uno de sus lados. Luego, se observa el número por el cual pasa el otro lado. Ese número de grados es la medida del ángulo.

Ejemplos: Medir con el transportador los siguientes ángulos: 50º, 140º, 135º, 90º, 180º.

Construye con el transportador y la regla , ángulos que midan: 45º, 120, 75º, 90º, 145º, 10º                                                                                                       

3. Se escribe  una letra griega  (  β, φ, δ ) o un número entre los lados del ángulo, cerca al vértice.

CONOCIMIENTOS BASICOS

Se llama ángulo a la región del plano comprendida entre dos semirrectas que tienen el mismo origen.

Las semirrectas son los lados del ángulo, y el origen común es el vértice del ángulo.

Un ángulo se puede simbolizar de las siguientes maneras:

< BAC  ó  < CAB   

1. Se marca un punto sobre cada lado del ángulo y se designan con letras mayúsculas. Luego se escriben las letras de los puntos dejando en el centro la del vértice.

< V

2. Se nombra solo el vértice (si no hay más ángulos con el mismo vértice)

                                                            

CONOCIMIENTO PREVIO

1.   ¿Qué es un ángulo para usted?

2.   ¿Cuáles son los elementos de un ángulo?

3.   ¿Cuántas clases de ángulos conoce usted?

4.   ¿Cómo y con que se mide un ángulo?



LA GEOMETRIA EN LA NATURALEZA



ANGULOS

ANGULO

ESTANDARES: 1.Identifica los ángulos como abertura en situaciones estáticas y dinámicas.

2. Distingue la clasificación de los ángulos de acuerdo a su medida y a su  posición

3. Construye la bisectriz de un ángulo dado.

COMPETENCIA: Capacidad de ubicarse en el espacio para establecer relaciones físicas y gráficas con entes geométricos.

INDICADORES DE LOGROS: 1. Mide ángulos con transportador y traza la bisectriz de un ángulo con regla y compás.

2. Construye con regla y compás, un ángulo congruente con otro ángulo dado.

3. Identifica ángulos según su posición y su medida.

4. Clasifica ángulos según su suma.

SEGMETOS Y RECTAS

SEGMENTOS CONGRUENTES: Dos segmentos son congruentes si tienen la misma medida.

AB ≡ CD.

RECTAS PARALELAS: Son dos rectas que pertenecen al mismo plano y que no se cortan, así se prolonguen.

L₁ ‖ L₂

_{RECTAS PERPENDICULARES: Dos rectas son perpendiculares si al cortarse forman cuatro ángulos iguales.}

SEMIRRECTA: Una semirrecta es una porciòn de recta que tiene un punto de origen pero no tiene final. Para nombrarla se marca el punto de origen y otro punto sobre ella. Luego se escriben las letras de los puntos con la flecha encima.

SEGMENTO: Es una porción de recta con inicio y final. Se simboliza marcando sus extremos y trazando un guión sobre ellos.

PUNTO MEDIO DE UN SEGMENTO: Un punto medio de un segmento es un punto que se encuentra entre sus extremos y los divide en partes iguales. AM = MB.

CLASES DE RECTAS

RECTAS COPLANARES: Son rectas que pertenecen a un mismo plano.

RECTAS SECANTES: Son aquellas que se cortan en un punto. El punto de intersecciòn pertenece a las dos rectas.

RECTAS CONCURRENTES: Se llaman rectas concurrentes a tres o màs rectas coplanares que se intersecan en el mismo punto.

VIDEO CONCEPTOS BASICOS DE GEOMETRIA

• PLANO: Nos da idea de plano, una hoja de papel, la superficie de una caja o el piso. Un plano se prolonga indefinidamente en todas las direcciones, està formado por infinitos puntos y no tiene grosor. Los planos se simbolizan con letras del alfabeto griego como α, β, Ω, Ø…
• Los puntos se pueden relacionar segùn su posiciòn, asì:

• Si los puntos pertenecen a la misma recta, se les llama colineales. Ejemplo los puntos A, B, C son colineales.

• Si los puntos pertenecen al mismo plano, se les llama coplanares. Los puntos P, Q, R son coplanares, pero P, Q, R no son coplanares con S. 

CONCEPTOS BASICOS

2. CONCEPTOS BASICOS
Los conceptos bàsicos de la geometrìa son: punto, recta y plano. Son tèrminos que no se pueden definir, solo se pueden tener idea de ellos.



 PUNTO: Nos da idea de punto la marca dejada por un làpiz bien afilado en una hoja de papel, el punto no tiene tamaño, solo tiene posiciòn. Los puntos se simbolizan con letras mayùsculas como A, B, C,... Ejemplo .A

• RECTA: Nos da idea de recta, un cordòn bien estirado o la marca que deja un làpiz al pasarlo por el borde de una regla. La lìnea recta està formada por una sucesiòn de puntos que se prolonga en una sola direcciòn. Para representar una recta, se trazan flechas, en ambos sentidos, esto indica que se prolonga indefinidamente. Para nombrar una recta, se marcan dos puntos sobre ella y se dibuja una dible flecha encima de las letras que los simbolizan. Tambièn se pueden nombrar con letras minùsculas.